Tangent Kernel of Deep Neural Network
Given the neural network with the struture as below:
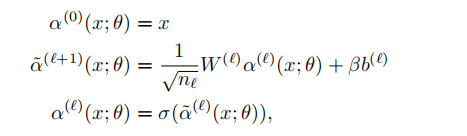
If we consider the inner product of the gradient for different input \(x\) and \(x^\prime\), given the width of the neural network is infiite, the inner product will be deterministic kernel dependending on the depth \(L\) and the non-linearity activation.


With the gradient, we can write down the linearization of the neural network.
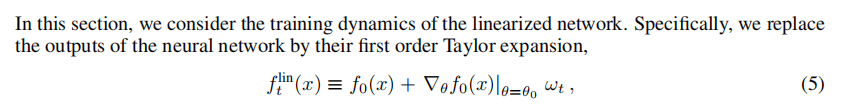
And then we can derive the expression of the linearization of the neural network during training.
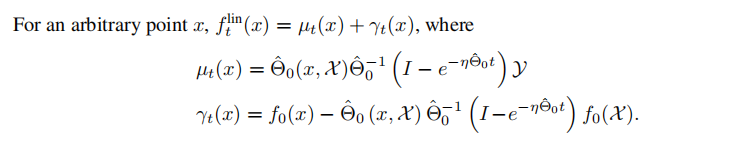
Given new testing point \(x\in X_T\), we can derive the distribution of the output of the trained linearization neural network as below
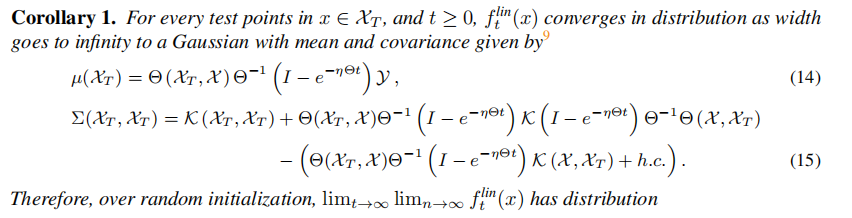
Results from paper Wide Neural Networks of Any Depth Evolve asLinear Models Under Gradient Descent claim that with the width of the neural network large enough, the neural network will be close to the linearization counterparts.