Deep Maxout Network GP

Investigating Neural Network with infinite width becomes a popular topic for two main reasons. First, neural networks in real application typically have a super large width structure which may share similar properties with infinite width neural network. Second, infinite width neural networks typically have analytical properties which are easier to study.

Infinite width neural network as Gaussain process(GP) was first derived in Neal(1996). Given a proper initialization, the output of one layer neural network becomes a GP with kernel depending on the nonlinearity activation. In Lee(2019),Matthews(2018), the infinite width deep neural network(DNN) as GP was derived and the kernel has a compositional structure depending on the number of depth and the nonlinearity activation in the network. Moreover, they found GP inference with DNN kernel often outperforms their finite width counterparts. Both Neal(1996). and Lee(2019)studied neural networks with activation applied on single linear combination of the input. Following the infinite width scheme, Novak(2018) and Garriga(2018) developed the GP kernel based on the deep convolutional neural networks(CNN) structure and Yang(2019) developed the GP kernel based on neural structures such as recurent neural networks(RNN), transformer etc.

Although it is widely utilized in application, the deep maxout network has never been derived as GP among previous works. The activation in maxout network applied on multiple linear combinations of the input(or previous layers) so that the the implementation in Neal(1996) and Lee(2017) can not directly apply here. In this work, we formally derive deep, infinite width maxout network as GP and characterize its corresponding kernel as a compositional structure. Moreover, we give a efficient method based on numerical integration and interpolation to implement the kernel. We apply the deep maxtout network kernel in GP regression inference on CIFAR10 dataset and it can achieve encouraging results in numerical study.

Review of Maxout network

Infinite width deep maxout network as Gaussian Process

Single-layer Case

Multi-layer Case

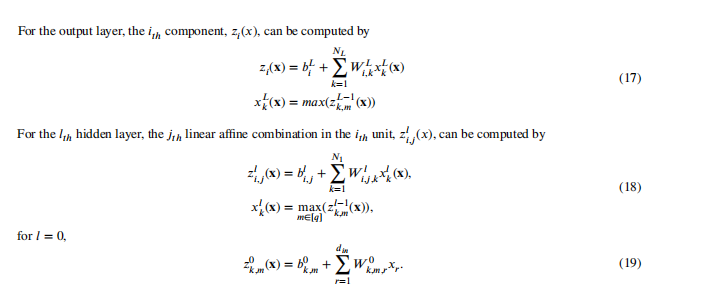
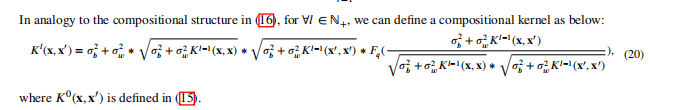
Doing Bayesian Inference with MNNGP

Numerical Experiment

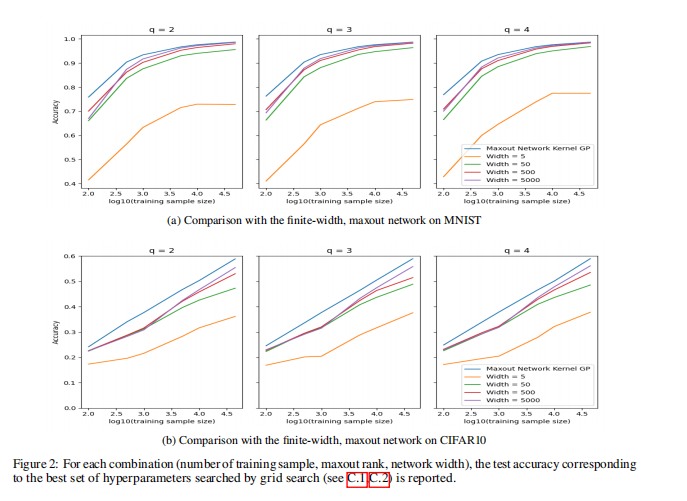
Compare with Finite width, deep maxout network

Based on the experiment, no matter how large the maxout rank is, we can find that the Bayesian inference based on the MNNGP almost always outperforms their finite-width counterparts. Moreover, as the width of the maxout network gets larger, the performance of the finite-width, maxout network will be closer to that of the MNNGP.

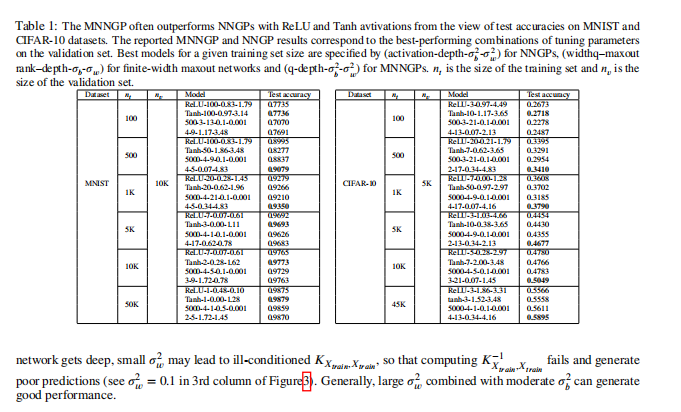
Compare with Deep Neural Network Kernel

We find that our MNNGP have competitive results compared with NNGPs with ReLU and Tanh kernels on MNIST and CIFAR10 datasets. Especially, our Deep Maxout Network Kernel always outperforms NNGPs in the more challenging dataset CIFAR10 with a significant improvement when the size of training set is large enough.

Reference:

Jaehoon Lee, Yasaman Bahri, Roman Novak, Samuel S Schoenholz, Jeffrey Pennington, and Jascha Sohl-Dickstein. Deep neural networks as gaussian processes. arXiv preprint arXiv:1711.00165, 2017.

Jaehoon Lee, Lechao Xiao, Samuel Schoenholz, Yasaman Bahri, Roman Novak, Jascha Sohl-Dickstein, and Jeffrey Pennington. Wide neural networks of any depth evolve as linear models under gradient descent. In H. Wallach,

H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox, and R. Garnett, editors, Advances in Neural Information Processing Systems, volume 32. Curran Associates, Inc., 2019. URL https://proceedings.neurips.cc/paper/ 2019/file/0d1a9651497a38d8b1c3871c84528bd4-Paper.pdf.

Yuan Cao and Quanquan Gu. Generalization bounds of stochastic gradient descent for wide and deep neural networks. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox, and R. Garnett, editors, Advances in Neural Information Processing Systems, volume 32. Curran Associates, Inc., 2019. URL https://proceedings.neurips. cc/paper/2019/file/cf9dc5e4e194fc21f397b4cac9cc3ae9-Paper.pdf.

Greg Yang, Jeffrey Pennington, Vinay Rao, Jascha Sohl-Dickstein, and Samuel S. Schoenholz. A mean field theory of batch normalization. CoRR, abs/1902.08129, 2019. URL http://arxiv.org/abs/1902.08129.

Radford M Neal. Priors for infinite networks. In Bayesian Learning for Neural Networks, pages 29–53. Springer, 1996. Alexander G de G Matthews, Mark Rowland, Jiri Hron, Richard E Turner, and Zoubin Ghahramani. Gaussian process behaviour in wide deep neural networks. arXiv preprint arXiv:1804.11271, 2018.

Roman Novak, Lechao Xiao, Jaehoon Lee, Yasaman Bahri, Greg Yang, Jiri Hron, Daniel A Abolafia, Jeffrey Pennington, and Jascha Sohl-Dickstein. Bayesian deep convolutional networks with many channels are gaussian processes. arXiv preprint arXiv:1810.05148, 2018.

Adrià Garriga-Alonso, Carl Edward Rasmussen, and Laurence Aitchison. Deep convolutional networks as shallow gaussian processes. arXiv preprint arXiv:1808.05587, 2018.

Greg Yang. Tensor programs I: wide feedforward or recurrent neural networks of any architecture are gaussian processes. CoRR, abs/1910.12478, 2019. URL http://arxiv.org/abs/1910.12478.

Ian Goodfellow, David Warde-Farley, Mehdi Mirza, Aaron Courville, and Yoshua Bengio. Maxout networks. In Proceedings of the 30th International Conference on Machine Learning, volume 28 of Proceedings of Machine Learning Research, pages 1319–1327, Atlanta, Georgia, USA, 17–19 Jun 2013. PMLR.

Youngmin Cho and Lawrence Saul. Kernel methods for deep learning. In Y. Bengio, D. Schuurmans, J. Lafferty, C. Williams, and A. Culotta, editors, Advances in Neural Information Processing Systems, vol- ume 22. Curran Associates, Inc., 2009. URL https://proceedings.neurips.cc/paper/2009/file/ 5751ec3e9a4feab575962e78e006250d-Paper.pdf.

Ryan Rifkin and Aldebaro Klautau. In defense of one-vs-all classification. The Journal of Machine Learning Research, 5:101–141, 2004.